The Physical Picture
With anything quantum mechanical, it can be hard to keep a physical picture in mind. Happily, basis set representations lend themselves nicely to a kind of interpretation that brings the physics back into the foreground. In this picture, rather than the classic
\[H = T + V\]we’ll move to
\[H = H^{(0)} + W\]where $H^{(0)}$ is a problem we’re already capable of solving and $W$ is an adjustment or “perturbation” of our original problem.
This might not look like much of a simplification (and it’s exactly equivalent), but it can often be helpful when you’re thinking about something physical.
For instance, let’s think about water, and we’ll even label the atoms
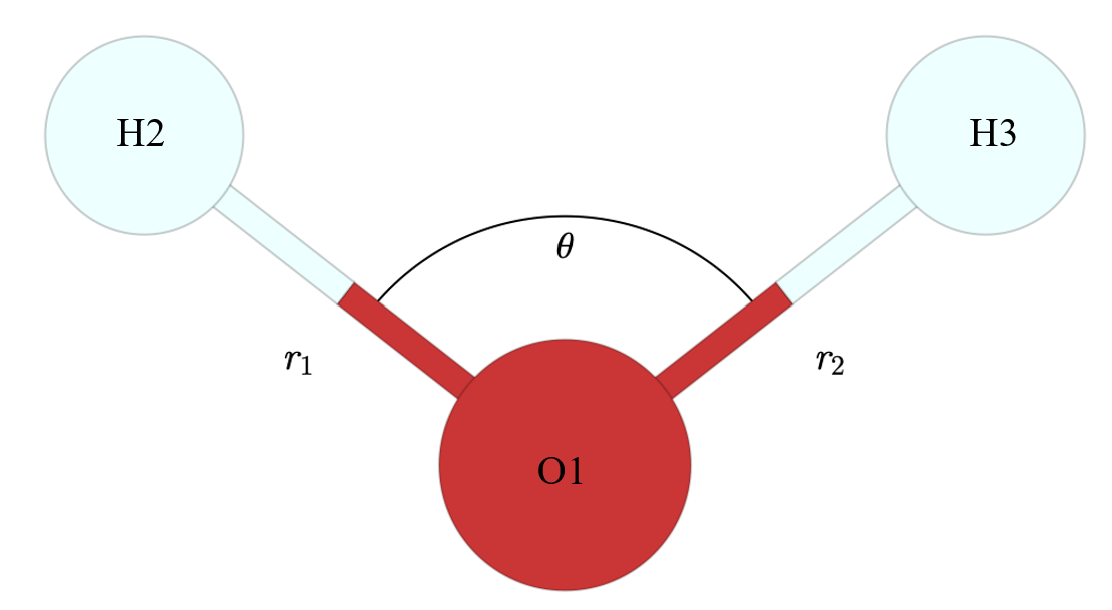
A common problem we’d ask ourselves is “what is the frequency of the vibration involving the stretching and contraction of the bond between O1 and H2?” Although it may feel trivial, when we pair these questions and results with experimental data we’re trying to make sense of what results can be really powerful. In addition, knowing how to ask these questions in a simpler context (like a bare water molecule) will be beneficial when moving on to real physically-relevant systems.
In any case, looking at that OH bond, other people have shown that it’s mostly well described by a harmonic oscillator model. We’ll get to what that is in a bit, but it actually doesn’t matter all that much. What’s more relevant is that we can use this initial model to simplify our analysis of this problem. To do that, we’ll write
\[H = H^{(H.O.)} + H^{(anh.)}\]which is to say, we’ll split our Hamiltonian into a purely harmonic portion and an anharmonic correction.
Then when we evaluate $H_{i,j}$, we get $H^{(H.O.)}_{i,j}$ for free and so all we need to work out is how to tackle $H^{(anh.)}$.
This still requires us to develop all the skills that we’d use to write out $H = T + V$, but it provides a conceptual simplification that makes the logic of the problem clearer, and problem solving is all about the logical flow.